Applications to life sciences, humanities and social sciences
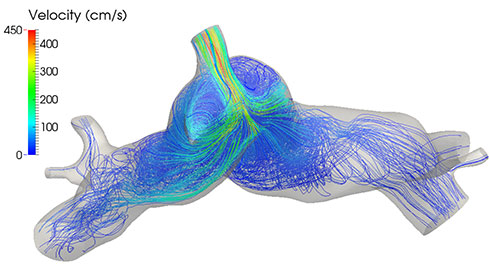
Tissue structure and growth models
The LJLL conducts research into the modeling of living tissues, integrating physics, mechanics and mathematics, with a focus on free-boundary systems and nutrient modeling. The focus is on surface tension effects and the correction of macroscopic models at the cellular level. The aim is to rigorously link macro and microscopic models via kinetic approaches, mean field, asymptotic studies and partial differential equation analysis.

Significant results have emerged in population modeling, with a focus on oscillatory behavior, entropy and heterogeneous polymerization. Phenotype-structured population modeling has applications in ecology, cellular evolution and evolutionary models of cancer. Collaborations with biologists enable the development and analysis of mathematical models for biological questions, with practical applications such as cell migration, cell cycle regulation, bacterial micro-colonies, tumor aggregate formation, vascular networks and adipose tissue dynamics. Recent work has focused on the interactions between the immune system and tumors, with particular reference to immunotherapy treatments.
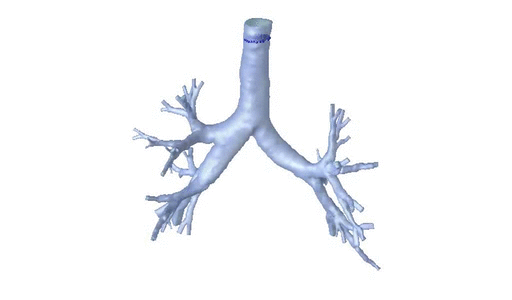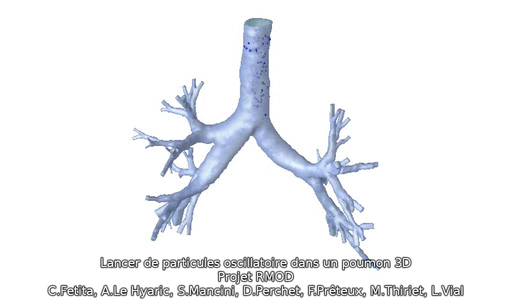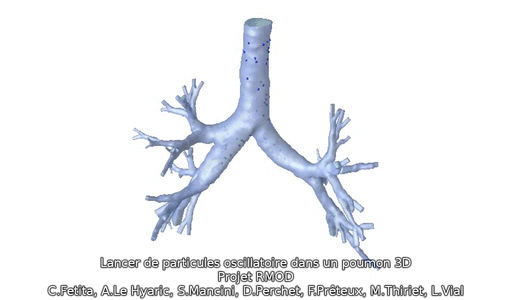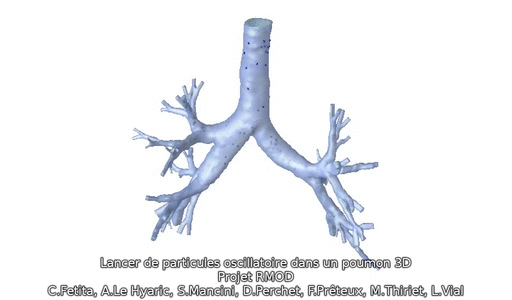
Mathematical models of the respiratory system
L. Boudin, C. Grandmont, F. Noël, and colleagues have developed a respiratory aerosol model that takes into account airway humidity and temperature variations, particularly for nanometric aerosols used in recent therapies.
In addition, C. Grandmont and colleagues have carried out work to describe ventilation and study the impact of carrier gases on respiration, using lung imaging data.

Mathematical models in hemodynamics
Mathematical models are used in hemodynamics to simulate the interaction between blood fluid and cardiac structure. To simplify simulations while maintaining reasonable accuracy, we use kinematic decoupling of hemodynamics and electromechanics, accompanied by reduced modeling of heart valve dynamics.

These simplified models can simulate blood flow patterns in the heart chambers with reduced computational costs, but they tend to neglect certain phases of the cardiac cycle.
A model called RIS (enhanced resistive immersed surface) has been proposed to solve this specific problem, taking into account the isovolumetric phases of the cardiac cycle. In parallel, a method commonly used in the medical field, called PISA (Proximal Isovelocity Surface Area), uses color Doppler echocardiography to estimate the severity of mitral regurgitation (leakage of blood in the opposite direction).
Mathematical models in neuroscience
The intersection between neuroscience and mathematics is of growing interest to mathematicians. Approaches range from differential equations to stochastic models, statistics and partial differential equations (PDEs). The challenges are many, including understanding the synchronization of neural networks and the emergence of spontaneous activity.

In the context of PDEs, kinetic Fokker-Planck-type mean-field models have been studied, in collaboration with LCQB (Institut de Biologie Paris Seine) and Beijing University. These models present difficulties related to boundary conditions and degeneracy, as well as transport equations.
A significant result in the field of neuroscience was obtained by D. Salort and D. Smets in collaboration with K. Ikeda and P. Roux. Smets in collaboration with K. Ikeda and P. Roux. They demonstrate that an approximated strongly inhibitory non-linear integrate-and-draw system can generate periodic solutions by taking into account the delay in synaptic connections. This result, initially observed numerically by physicists, constitutes the first analytical proof of the existence of such solutions.
Population dynamics and control in ecology and epidemiology
In ecology and epidemiology, population dynamics and control are mainly modelled by reaction equations. A first theme is the study of the general properties of the solutions of these equations, particularly in heterogeneous media. The focus is on applications in ecology and epidemiology, with a particular interest in optimizing population survival by influencing the location of resources.

Work includes problems related to shape optimization and optimal control, with concrete applications such as the control of populations of disease vectors or agricultural pests, in particular mosquito vectors of diseases such as Dengue, Zika and Chikungunya. Interesting mathematical results have been obtained, particularly with regard to optimal control and feedback control of these systems.
Research is expanding from models based on ordinary differential equations (ODEs) to partial differential equation (PDE) models that take into account the spatial component, climatic variations and population structuring. Current work focuses on optimizing mosquito release strategies, highlighting the relationship between travel speed, release strip width and the quantity of mosquitoes used.
In epidemiology, researchers have also explored more general models, including heterogeneous extensions of Kermack and McKendrick’s SIR model, studying the existence of propagation waves in heterogeneous settings. In addition, work has been carried out on the mathematical modelling of territoriality in predators, showing that the formation of territories is advantageous in certain situations.
