Applications aux sciences du vivant, sciences humaines et sociales
Modèles de structure et de croissance de tissus
Le LJLL mène des recherches en modélisation des tissus vivants, intégrant physique, mécanique et mathématiques, avec un accent sur les systèmes à frontière libre et la modélisation des nutriments. L’attention est portée sur les effets de tension de surface et la correction des modèles macroscopiques à l’échelle cellulaire. L’objectif est de lier rigoureusement les modèles macro et microscopiques via des approches cinétiques, champ moyen, études asymptotiques et analyse des équations aux dérivées partielles.

Des résultats significatifs ont émergé dans la modélisation de populations, avec un intérêt pour les comportements oscillants, l’entropie et la polymérisation hétérogène. La modélisation de populations structurées en phénotype a des applications en écologie, évolution cellulaire et modèles évolutifs du cancer. Les collaborations avec des biologistes permettent le développement et l’analyse de modèles mathématiques pour des questions biologiques, avec des applications pratiques telles que la migration cellulaire, la régulation du cycle cellulaire, les micro-colonies bactériennes, la formation d’agrégats tumoraux, les réseaux vasculaires et la dynamique du tissu adipeux. Des travaux récents se sont concentrés sur les interactions entre le système immunitaire et les tumeurs, notamment pour les traitements par immunothérapies.
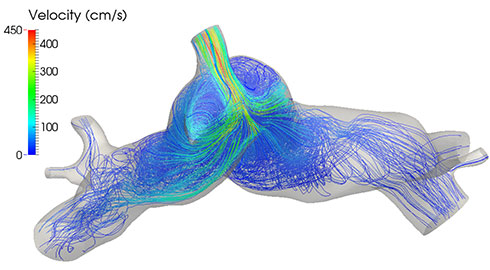
Modèles mathématiques du système respiratoire
L. Boudin, C. Grandmont, F. Noël, et leurs collaborateurs ont développé un modèle d’aérosol respiratoire prenant en compte l’humidité des voies aériennes et les variations de température, notamment pour les aérosols nanométriques utilisés dans des thérapies récentes.
Par ailleurs, C. Grandmont et ses collaborateurs ont réalisé des travaux pour décrire la ventilation et étudier l’impact des gaz porteurs sur la respiration, en utilisant des données d’imagerie pulmonaire.

Modèles mathématiques en hémodynamique
Des modèles mathématiques sont utilisés en hémodynamique pour simuler l’interaction entre le fluide sanguin et la structure cardiaque. Pour simplifier les simulations tout en conservant une précision raisonnable, on a recours à un découplage cinématique de l’hémodynamique et de l’électromécanique, accompagné d’une modélisation réduite de la dynamique des valves cardiaques.

Ces modèles simplifiés permettent de simuler les schémas d’écoulement sanguin dans les cavités cardiaques avec des coûts de calcul réduits, mais ils ont tendance à négliger certaines phases du cycle cardiaque.
Un modèle appelé RIS (enhanced resistive immersed surface) a été proposé pour résoudre ce problème spécifique en prenant en compte les phases isovolumétriques du cycle cardiaque. En parallèle, une méthode couramment utilisée dans le domaine médical, appelée PISA (Proximal Isovelocity Surface Area), utilise l’échocardiographie Doppler couleur pour estimer la sévérité de la régurgitation mitrale (fuite de sang dans le sens inverse).
Modèles mathématiques en neurosciences
L’intersection entre les neurosciences et les mathématiques suscite un intérêt croissant parmi les mathématiciens. Les approches varient, allant des équations différentielles aux modèles stochastiques, en passant par la statistique et les équations aux dérivées partielles (EDP). Les défis sont nombreux, notamment la compréhension de la synchronisation des réseaux neuronaux et l’émergence d’activité spontanée.

Dans le contexte des EDP, des modèles de champ moyen de type Fokker-Planck cinétiques ont été étudiés, en collaboration avec le LCQB (Institut de Biologie Paris Seine) et l’Université de Beijing. Ces modèles présentent des difficultés liées aux conditions aux limites et à la dégénérescence, ainsi que des équations de transport.
Un résultat significatif dans le domaine des neurosciences a été obtenu par D. Salort et D. Smets en collaboration avec K. Ikeda et P. Roux. Ils démontrent qu’un système approché de type intègre-et-tir non-linéaire fortement inhibiteur peut générer des solutions périodiques en prenant en compte le retard dans les connexions synaptiques. Ce résultat, initialement observé numériquement par des physiciens, constitue la première preuve analytique de l’existence de telles solutions.
Dynamique et contrôle de populations en écologie et épidémiologie
La dynamique et le contrôle des populations en écologie et épidémiologie, sont principalement modélisés par des équations de réaction. Une première thématique est l’étude des propriétés générales des solutions de ces équations, en particulier dans des milieux hétérogènes. L’accent est mis sur les applications en écologie et épidémiologie, avec un intérêt particulier pour l’optimisation de la survie des populations en agissant sur l’emplacement des ressources.

Les travaux incluent des problèmes liés à l’optimisation de forme et au contrôle optimal, avec des applications concrètes telles que le contrôle des populations de vecteurs de maladies ou de ravageurs agricoles, en particulier les moustiques vecteurs de maladies comme la Dengue, le Zika et le Chikungunya. Des résultats mathématiques intéressants ont été obtenus, notamment en ce qui concerne le contrôle optimal et le contrôle feedback de ces systèmes.
Les recherches s’étendent à des modèles basés sur des équations différentielles ordinaires (EDO) vers des modèles d’équations aux dérivées partielles (EDP) prenant en compte la composante spatiale, les variations climatiques, et la structuration de la population. Les travaux actuels portent sur l’optimisation des stratégies de lâchers de moustiques, mettant en évidence la relation entre la vitesse de déplacement, la largeur de la bande de lâchers, et la quantité de moustiques utilisée.
En épidémiologie, les chercheurs ont également exploré des modèles plus généraux, notamment des extensions hétérogènes du modèle SIR de Kermack et McKendrick, étudiant l’existence d’ondes de propagation dans des cadres hétérogènes. Par ailleurs, des travaux ont été réalisés sur la modélisation mathématique de la territorialité chez les prédateurs, montrant que la formation de territoires est avantageuse dans certaines situations.
