Applications à la physique, chimie, mécanique et ingénierie





Les activités du Laboratoire Jacques-Louis Lions peuvent aussi être présentées du point de vue de leurs applications, qui sont multiples et recouvrent toutes les échelles intervenant en physique théorique et en physique appliquée. Nous présentons ici un panel non-exhaustif de résultats représentatifs.
Chimie quantique
Résultats principaux
Mi-Song Dupuy, Eric Cancès et Xavier Blanc ont mis au point des méthodes de calcul de structures électroniques utilisant des bases d’ondes planes augmentées de fonctions décrivant précisément les singularités des fonctions d’onde. Yvon Maday et ses collaborateurs ont obtenu une série de résultats sur l’analyse a posteriori de l’erreur pour des problèmes au valeurs propres non linéaires comme ceux que l’on rencontre en calcul de structure électronique (Hartree Fock ou Kohn-Sham. Pierre Monmarché a développé des algorithmes stochastiques pour échantillonner des systèmes de chimie biologique, en collaboration avec des chimistes et des physiciens pour la dynamique moléculaire.
Perspectives actuelles
Les algorithmes adaptatifs développés par Pierre Monmarché en dynamique moléculaire sont à un niveau de maturité où l’on va pouvoir les appliquer à des problèmes non-convexes en grande dimension d’autres domaines, notamment l’optimisation des réseaux de neurones en apprentissage profond.
Mi-Song Dupuy souhaite étudier deux nouveaux aspects de la simulation numérique des systèmes chimiques. Le premier porte sur l’analyse de la théorie de la fonctionnelle densité dépendante du temps (TDDFT) qui a pour but de calculer de manière efficace les états excités d’un système électronique. Un second volet porte sur les réseaux de tenseurs pour les problèmes en grande dimension, notamment sur la question de la suprémacie de l’ordinateur quantique.
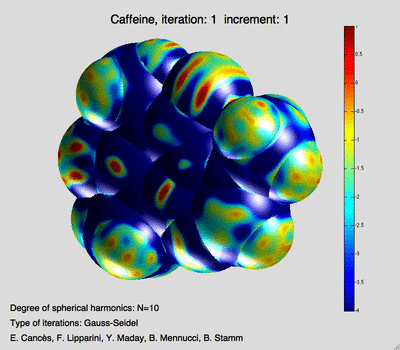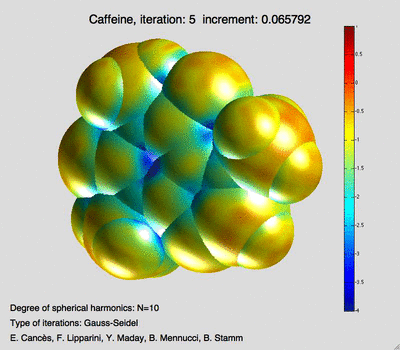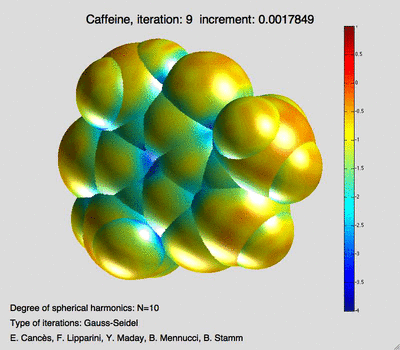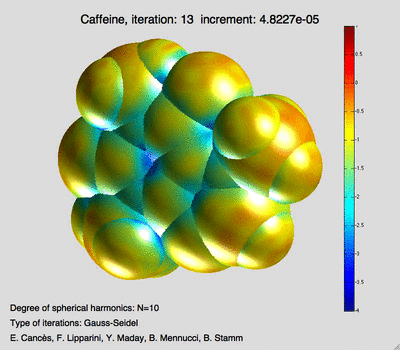
Mécanique des fluides
Résultats principaux
Xavier Blanc a étudié l’effet d’un rayonnement intense sur le développement d’instabilités hydrodynamiques dans des écoulements stellaires dans le régime d’un petit nombre de Péclet. Frédérique Charles et ses collaborateurs s’intéressent à l’évolution de particules (telles que des particules solides de poussière ou des gouttelettes) dans un gaz raréfié. L’interaction entre le gaz et les particules de poussières est modélisée par une équation de transport libre en domaine mouvant.
Perspectives actuelles
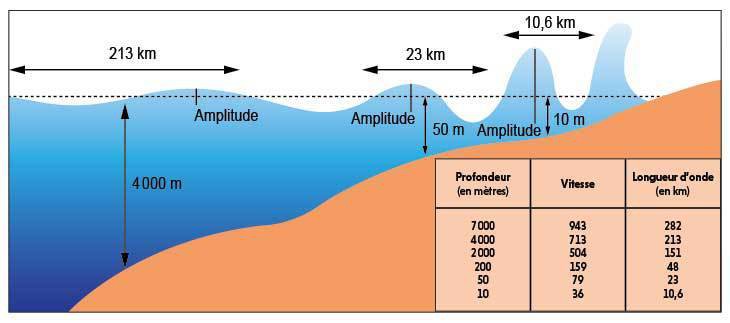
Les travaux de Jacques Sainte-Marie ont mené au développement du code numérique Freshkiss3d pour la résolution des équations de Navier-Stokes à surface libre (voir [24] et https://freshkiss3d.gitlabpages.inria.fr). Cet outil est très utile pour l’interaction avec les océanographes et l’amélioration des codes numériques utilisés de façon opérationnelle notamment le code NEMO https://www.nemo-ocean.eu/. Ceci constituera l’axe majeur des recherches menées dans les années à venir.
Modélisation des solides
Résultats principaux
Hervé Le Dret a revisité les fondements de la thermodynamique des milieux continus et la modélisation mathématique des matériaux thermo-visco-élastiques avec ou sans variables internes. Stéphane Labbé a développé des modèles atomiques de matériaux ferromagnétiques pour comprendre les phénomènes de température et leur intégration dans des modèles mésoscopiques micro-magnétiques.
Relativité générale
Résultats principaux
Philippe LeFloch étudie la stabilité des espaces-temps de la relativité générale. En collaboration avec son ancien doctorant Yue Ma, pour les équations d’Einstein couplées avec un champ massif, tel un champ scalaire de Klein-Gordon. Jérémie Szeftel s’est intéressé à la conjecture de stabilité des trous noirs de Kerr, qui forment une famille de solutions stationnaires explicites des équations d’Einstein dans le vide correspondant à des trous noirs en rotation. Jacques Smulevici a démontré l’existence de solutions stationnaires dans des géométries représentant des trous noirs axisymétriques, avec des outils de théorie cinétique.
Perspectives actuelles
Les activités du laboratoire sur la relativité générale mathématique continuent à se développer. En particulier, Philippe LeFloch a lancé un nouveau thème de recherche sur les contraintes (hamiltonienne, moment) associées aux équations d’Einstein, pour lesquelles il développe de nouvelles techniques d’analyse géométrique pour les EDP elliptiques non-linéaires.

