Software developed in the laboratory

ddCOSMO

“ddCOSMO is a recently proposed algorithm to solve the polarization equation for the Conductor-like Screening Model (COSMO), a popular Continuum Solvation Model. Traditional implementations of Continuum Solvation Models, including COSMO and the Polarizable Continuum Model (PCM), are based on a Boundary Element Method (BEM) discretization of the associated integral equation and require the solution of a large, dense linear system of equations : while fast summation techniques such as the Fast Multipole Method can be used in iterative solvers, the computational task can easily be quite formidable for large systems. Furthermore, the most recent discretizations are controlled by a large number of parameters and are therefore difficult to control.”

For more information, please contact Yvon Maday.

FELiScE

(Finite Elements for Life Sciences and Engineering) is a parallel finite element library written in C++ developped by Inria team Comedia. The library provides an unified software environment for the development of state-of-the-art finite element solvers for the spatial discretization of partial differential equations (PDE) in 1D, 2D and 3D spatial dimensions.

FreeFem++

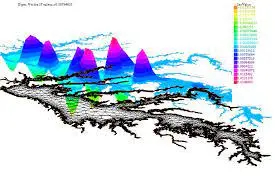
Chesapeake FreeFEM

A PDE solder developed by Frédéric Hecht & Antoine Le Hyaric.

“FreeFem++ is a partial differential equation solver. It has its own language. freefem scripts can solve multiphysics non linear systems in 2D and 3D.

Problems involving PDE (2d, 3d) from several branches of physics such as fluid-structure interactions require interpolations of data on several meshes and their manipulation within one program. FreeFem++ includes a fast 2^d-tree-based interpolation algorithm and a language for the manipulation of data on multiple meshes (as a follow up of bamg (now a part of FreeFem++ ).

FreeFem++ is written in C++ and the FreeFem++ language is a C++ idiom. It runs on Macs, Windows, Unix machines. FreeFem++ replaces the older freefem and freefem+.”

Freshkiss3d

For more information, please contactJacques Sainte-Marie and Fabien Souille.

“FREe Surface Hydrodynamics using KInetic SchemeS” : simulation of free surface fluid flows (Navier-Stokes)

  • language : Cython (Python + C)
  • license : GPL
  • property : Inria – CEREMA – UPMC

HPDDM

Developed by Pierre Jolivet and Frédéric Nataf.

“HPDDM is an efficient implementation of various domain decomposition methods (DDM) such as one- and two-level Restricted Additive Schwarz methods, the Finite Element Tearing and Interconnecting (FETI) method, and the Balancing Domain Decomposition (BDD) method. These methods can be enhanced with deflation vectors computed automatically by the framework using :

Generalized Eigenvalue problems on the Overlap (GenEO), an approach first introduced in a paper by Spillane et al., or
local Dirichlet-to-Neumann operators, an approach first introduced in a paper by Nataf et al. and revisited by Conen et al.
This code has been proven to be efficient for solving various elliptic problems such as scalar diffusion equations, the system of linear elasticity, but also frequency domain problems like the Helmholtz equation. A comparison with modern multigrid methods can be found in the thesis of Jolivet. The preconditioners may be used with a variety of Krylov subspace methods (which all support right, left, and variable preconditioning) :

GMRES and Block GMRES,
CG, Block CG, and Breakdown-Free Block CG,
GCRO-DR and Block GCRO-DR.

Medit

A scientific vizualisation package by Pascal Frey.

“OpenGL-based scientific visualization software. Developped to visualize numerical simulation results on unstructured meshes in two and three dimensions. Scalar, vector and tensor fields can be easily associated and displayed with meshes.”

mu-diff

Mudiff

Developed by Bertrand Thierry et Xavier Antoine.

Mu-diff (acronym for MUltiple-DIFFraction) is an open-source Matlab toolbox for solving multiple scattering problems by clusters of circular cylinders. Multiple scattering is a highly complex wave problem that finds great applications in many areas of physics and engineering (acoustics, electromagnetism, optics, nanophotonics, elasticity…). Any distribution of the cylinders is possible, deterministic or random, allowing to define basic to complex disordered media. The rigorous mathematical formulation is based on the integral equations formulations. The finite-dimensional approximation technique is a Fourier spectral method combined with linear algebra solvers (direct gaussian elimination method or preconditioned Krylov subspace iterative techniques). Pre- and post-processing facilities are included in mu-diff. Since integral equations are used, many direct and inverse wave scattering problems can be solved with mu-diff. Examples of scripts are provided with the toolbox along with a user-guide.

SeLaLib

SeLaLib

Martin Campos-Pinto and Antoine Le Hyaric participate in the development of Selalib.

“The SeLaLib software library is a modular library for kinetic and gyrokinetic simulations of plasmas in fusion energy devices by semi-Lagrangian or particle-in-cell methods.

The SeLaLib project arose from the need of researchers to develop numerical methods with simplified test cases while also having independently tested modules that would facilitate gradual changes in existing production code. While originally envisioned to be specialized on the semi-lagrangian method, the abstractions that has been built can be used with other types of approaches, such as particle-in-cell.

The SeLaLib project started in Strasbourg in collaboration between the TONUS INRIA team, the department IRMA at Université de Strasbourg, CEA Cadarache and CNRS. The basis of the library was developed by an INRIA research engineer, Edwin Chacon Golcher, during 2011-2014. A software engineer, Pierre Navaro, from CNRS has been and continues to be responsible for the infrastructure of the project, besides being
involved in the development and design of the library. In 2012, researchers from Max-Planck IPP joined the development of the SeLaLib library.

SeLaLib contains a collection of individual building blocks for the parallel simulation of the Vlasov equations and the gyrokinetic equation either based on semi-Lagrangian schemes or particle methods. Besides numerical algorithms the library provides low-level utilities, input-output modules as well as parallelization strategies. Moreover, a collection of simulations for typical test cases with various

ppfem

FEM with ppform splines in MATLAB by Roman Andreev.

“ppfem is a collection of MATLAB routines for the finite element method (FEM) with piecewise polynomial splines (aka isogeometric analysis) in 1d. The idea of the package is to facilitate prototyping on tensor product meshes — at the possible cost of assembly speed.

  • For maximum flexibility, the basis functions are constructed explicitly and stored in the MATLAB ppform.
  • Spaces based on different spatial meshes and local polynomial degrees can be mixed, for instance in constructing Gramians.
  • Some common spline spaces are provided (B-splines, continuous piecewise polynomials, Babuska—Shen, …).
  • Homogeneous boundary conditions of any kind and order can be easily implemented.
  • Load vectors for n-variate functions on product meshes can be constructed.”

Mefisto

Finite element software by Alain Perronnet.

“This software was designed, developed and is maintained by Alain Perronnet. Numerous meshing modules, linear system solver modules, sub-domain modules and so on, were designed and developed by Pascal JOLY. The structured algebraic and elliptic quadrangulators and hexahedronizers and the PostScript graphics output were designed and developed by Christophe Doursat. Several graduate students also developed modules. The software was written at the Laboratoire Jacques-Louis Lions.”

Online courses and documents

Other software

A list of software used by lab members. Internal support by Antoine Le Hyaric.